Для того чтобы конденсатор зарядить, необходимо подключить его к источнику питания электрической энергии. Во время заряда происходит поляризация диэлектрика, создается электрическое поле между пластинами, обусловленное электрическими зарядами и в поле запасается энергия.
Повышение напряжения между пластинами увеличивает количество электричества. Между напряжением и зарядом существует линейная зависимость
,
где C электрическая емкость (смотрите рисунок)
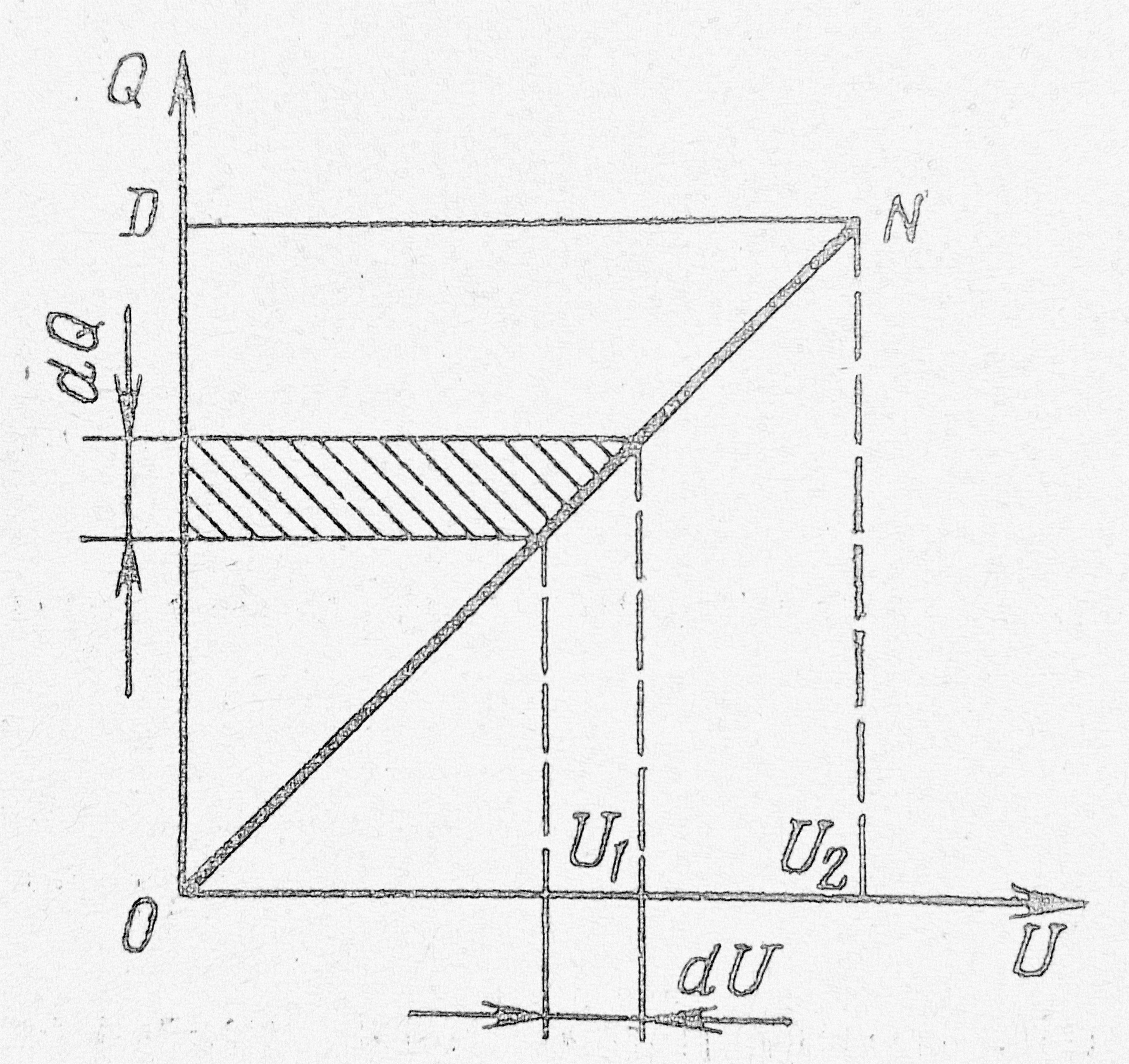
За очень маленький промежуток времени dt электрический заряд изменится на малое приращение dQ, поэтому заштрихованную площадь на графике можно определить как площадь прямоугольника, равную dS=U₁ dQ=dA
т. е. бесконечно малой работе, совершаемой в электрическом поле. Если же увеличивать напряжение между пластинами конденсатора от O до U₂,
то вся работа будет численно равна энергии электрического поля конденсатора.
Вся энергия электрического поля за время заряда конденсатора определяется площадью треугольника ODN, и поэтому
,
где
.
При разряде конденсатора энергия его электрического поля превращается в тепловую.
В системе СИ энергия электрического поля измеряется в джоулях (Дж). В электронике применяют единицу измерения энергии, называемую электрон-вольт (эВ). Электрон вольт равен работе, которую совершают силы поля, перемещая заряд, равный заряду электрона
Кл), между двумя точками поля с разностью потенциалов между ними один вольт:
1 эВ=1,6 · 10⁻¹⁹ Кл · 1В=1,6×10⁻¹⁹ Дж
Пример. Конденсатор емкостью 10 пФ подключен к источнику с напряжением 100В. Определить энергию электрического поля конденсатора.
Решение:
Дж.